Home > Kryptographie > Zufallsgeneratoren
Kryptographie
Wir haben die sog. Zufallsgeneratoren schon in den vorherigen Kapiteln teilweise kennen gelernt. RC4 ist z. B. solch ein Generator. In diesem Kapitel wollen wir uns näher damit beschäftigen: Was ein Zufallsgenerator ist und wie er funktioniert.
Ich werde jetzt eine These in den Raum stellen, die ich im Verlaufe dieses Kapitels zu belegen versuche:
Das Erzeugen echter Zufallsfolgen ist mit dem Computer unmöglich.
Klingt ziemlich entmutigend, oder ...? Dabei bieten uns Programmiersprachen doch schon ziemlich viele Zufallsgeneratoren. In C gibt es z. B. die rand()-Funktion, die mit randomize() initialisiert wird. Wie erzeugt der Computer diese Zahlen überhaupt? Die Antwort ist einfach: Er berechnet sie! Es handelt sich bei diesem Generator um einen sog. linearen Kongruenzgenerator (LCG), der die Form
Xn = (a · Xn − 1 + b) mod m
hat. Der erste Wert in dieser Folge, X0, wird mittels srand() bzw. randomize() gesetzt (dies ist der "Schlüssel"). Die Variablen a, b und m sind konstant: a ist der Multiplikator, b das Inkrement und m der Modul. Wurden diese drei Variablen gut gewählt, so hat der Generator die maximale Periode von m. Das heißt, der Generator wird sich nach m Ausgaben von Zufallszahlen wiederholen. Zum Beispiel hat der folgende fiktive Generator eine Periode von 10:
14159265351415926535 usw.
Der C-Zufallsgenerator hat eine Periode von 232, d. h. nach 232 (ca. 4,2 Milliarden) Ausgaben wird die Sequenz sich wiederholen.
Ein Beispiel für einen weiteren linearen Kongruenzgenerator ist:
Xn = (106 · Xn − 1 + 1283) mod 6075
Dieser Zufallsgenerator hat eine Periode von nur 6075. Die Zufallsfolge dieses Generators würde lauten:
X0 = 17
(Xn) = 3085; 243; 2741; 229; 1257; ...
Obwohl solche Generatoren gute statistische Eigenschaften aufweisen, sind sie leider nicht sicher, da sie vorhersagbar sind. Auch Modifikationen der Generatoren sind allesamt nicht für kryptographische Zwecke geeignet. Daher sollten Kongruenzgeneratoren in der Kryptographie auf gar keinen Fall benutzt werden.
Computer können Zufallsfolgen nur berechnen. Man füttert sie mit einem bestimmten Startwert (Seed) und lässt sich dann eine bestimmte Anzahl von Zufallszahlen ausgeben. Als Seed kann z. B. die Systemzeit, Position des Mauszeigers, Mausbewegungen, eine Kopie jedes Tastendrucks, CPU-Auslastung etc. verwendet werden. Mit einem Aufruf der C-Funktion randomize() wird der Kongruenzgenerator mit der Systemzeit initialisiert. Natürlich gibt es weitaus bessere Generatoren. Sie sollten sich jedoch darüber im Klaren sein, dass Pseudozufallsgeneratoren, gleich, wie gute "Seeds" sie verwenden, zu knacken sind – jedenfalls theoretisch. Das liegt daran, dass Computer absolut deterministisch sind, d. h., sie sind voraussehbar. Wenn ich am einen Ende etwas hineinschiebe, kann ich berechnen, was am andern Ende dabei herauskommt. Wenn ich zweimal dasselbe hineinschiebe, kommt auch zweimal dasselbe raus. Ist etwas voraussehbar, kann es nicht zufällig sein.
Nun ist die Frage: Gibt es "echten" Zufall überhaupt? Die Antwort ist: Ja. Das wissen wir aus der Quantenmechanik. Ferner muss bei einem "echten" Zufallsgenerator Folgendes gewährleistet sein:
Von einem Computer-Generator werden mindestens die ersten beiden Eigenschaften verlangt; die dritte kann ja aufgrund der deterministischen Eigenschaften des Computers nicht erfüllt werden. Da die vom Computer erzeugten Zahlen nicht wirklich "zufällig" ist ("pseudozufällig"), nennt man solche Generatoren auch Pseudo-Zufallsgeneratoren oder Pseudo Random Number Generators (PRNG).
Wohlgemerkt, es gibt durchaus recht gute Computer-Verfahren zur Erzeugung pseudozufälliger Sequenzen, z. B. die Messung der Zeit zwischen zwei aufeinanderfolgenden Tastaturanschlägen, wie es beispielsweise PGP macht. Allerdings könnten bestimmte Filter oder andere Mechanismen das Ergebnis, welches beim Programm ankommt, verfälschen.
Nun, es gibt ja nicht nur Computer-Algorithmen zum Erzeugen von Zufallszahlen. Man könnte z. B. einen 128-Bit-Schlüssel erzeugen, indem man 128-mal eine Münze wirft. "Kopf" entspricht dabei der binären 0 und "Zahl" der binären 1. Oder ich würfle. Jede gerade Zahl entspricht einer 0, jede ungerade einer 1. Diese Verfahren sind sicher, weil sie unglaublich schwer voraussagbar sind. Warum? Das erzeugte Zufallsbit hängt von so vielen Faktoren ab, dass es unmöglich ist, es vorauszusagen. Zudem "initialisiere" ich das Verfahren ja mit jedem Wurf neu. Ich berechne also nichts, sondern verlasse mich auf die Chaos-Theorie. Die dritte Eigenschaft ist zwar dadurch nicht erfüllt, jedoch wird niemand den Wurf reproduzieren können, sofern er nicht in exakt derselben Weise wirft bzw. würfelt wie ich es getan habe (bedenken Sie die enorme Anzahl von Faktoren, von denen das Ergebnis eines Wurfes abhängt!). Diese Verfahren sind also sicher, sofern man einigermaßen "vernünftig" wirft.
Als Beispiel habe ich einmal folgende 128-Bit-Zufallszahl erzeugt, indem ich mit Hilfe des oben beschriebenen Verfahrens 128-mal eine Münze geworfen habe:
0100101101111011 0000111101101001 1110010101101101 0000101101100100 1110001111001001 1001100001100001 1011011101100101 0010000110110111
Wenn ich mich nicht verzählt habe, kommt 67x die "1" vor, das entspricht einer Häufigkeit von ca. 52,3 Prozent. Nullen und Einsen sind also fast gleichmäßig verteilt. So, nun versuchen Sie mal, dieses Ergebnis zu reproduzieren. ;-) Nur keine Sorge: Die Chance dafür, dass Sie denselben Schlüssel erwürfeln, ist in etwa so hoch wie die Chance auf einen 5,8-maligen Lotto-Hauptgewinn in Folge.
Lineare Kongruenzgeneratoren sind ja leider nicht geeignet für unsere äußerst anspruchsvollen Zwecke. Wir brauchen Generatoren, die die ersten beiden Bedingungen erfüllen. Wieso greifen wir nicht einfach auf unsere modernen kryptographischen Verschlüsselungs-Algorithmen zurück? Dann könnte man z. B.
der Seed-Wert fungiert dabei als Schlüssel. Beim Blockalgorithmus kann der Initialisierungs-Vektor ein beliebiger Wert, z. B. 0, sein. Derartige Zufallsgeneratoren sind sicher, wenn der kryptographische Algorithmus sicher ist. RC4 scheint besonders gut geeignet zu sein: Er hat eine Periode von ca. 10100 (!) und besteht laut RSA Security alle statischen Tests.
Ein lineares Schieberegister (linear feedback shift register, kurz LFSR) besteht aus einer bestimmten Anzahl von Zellen, in denen jeweils ein Bit gespeichert wird. In einem gewissen Takt werden die Bits durch das Register hindurchgeschoben. Dieses Beispiel sollte es verdeutlichen:
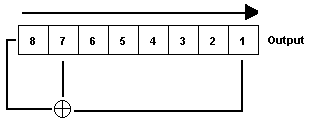
Dieses Schieberegister besteht aus 8 Zellen, die von hinten durchnummeriert werden. Das Ganze funktioniert wie folgt: Das 1. und das 7. Bit werden "angezapft" und einer bestimmten Rückkopplungsfunktion f übergeben, deren Ergebnis in die 8. Zelle gelangt, wobei das gesamte Register nach rechts verschoben wird, also das Bit der 8. Zelle in die 7. Zelle, das Bit der 7. Zelle in die 6. usw. Das Bit in der 1. Zelle ist das Ausgabebit (Output). In unserem Fall ist die Rückkopplungsfunktion ein einfaches xor. Bevor Zufallsbits ausgegeben werden können, muss das Register mit einem bestimmten Wert initialisiert werden (Schlüssel), d. h. jede Zelle erhält ein Initialisierungs-Bit. Wenn alle Zellen auf 0 gesetzt sind, gibt das LFSR natürlich nur Nullen aus; daher sollte dieser Zustand vermieden werden.
Wie bei jedem PRNG wird sich die Folge der Ausgabebits irgendwann wiederholen. Ein n-Bit-LFSR kann einen von 2n − 1 (nicht 2n, da ja der Zustand von lauter Nullen bewirkt, dass das LFSR nur noch Nullen ausgibt) internen Zuständen annehmen. Das bedeutet, dass es theoretisch eine Pseudozufallssequenz der Länge 2n − 1 generieren kann, bevor eine Wiederholung auftritt. Ob das LFSR diese maximale Periode hat, hängt davon ab, wo die Bits angezapft werden. Wenn wir bei unserem Beispiel die Bits also an ganz bestimmten Stellen anzapfen, können wir die maximale Periode von 28 − 1 = 255 erreichen. Wo man nun genau Bits anzapfen muss, wollen wir jetzt nicht näher besprechen, da dies mit komplizierter mathematischer Theorie zu tun hat. Hauptsache, Sie wissen einigermaßen, was lineare Schieberegister jetzt sind. ;-)
Welche Bedeutung haben Schieberegister in der Kryptographie? Zunächst sei einmal zu sagen, dass es unzählige Arbeiten über diesen Themenbereich gibt. Diese Form der Mathematik scheint recht beliebt zu sein, vor allem in der Kryptographie. Es gibt auch Algorithmen, die auf Basis dieser Schieberegister arbeiten, aber fast ausnahmslos unsicher sind. Zudem sind sie auch noch sehr langsam. Wenn Sie mich fragen: LFSRs sind nicht der Weisheit letzter Schluss. Ich würde auf den Einsatz von linearen Schieberegistern als PRNGs ganz verzichten. Es gibt schnellere und bessere, sprich sicherere, Alternativen. Irgendwo da draußen. :-)
Bei diesem PRNG (auch BBS abgekürzt und gelegentlich als "quadratische Restgenerator" bezeichnet) handelt es sich um einen recht einfachen, auf großen Zahlen basierenden Zufallsgenerator. Dabei sucht man zunächst zwei große Primzahlen p und q, welche kongruent 3 modulo 4 sind, d. h.:
p mod 4 = 3
(selbiges gilt für q)
Dann bildet man das Produkt n:
n = pq
(n ist übrigens eine sog. Blumsche Zahl.) Nun benötigen wir noch eine Zahl x, die zu n relativ prim ist; d. h., x hat keine gemeinsamen Teiler außer 1 mit n (Beispiel: 21 [3 · 7] ist relativ prim zu 10 [2 · 5]). Um den Generator zu starten, wird der Startwert x0 berechnet:
x0 = x2 mod n
Jetzt kann's losgehen. Das i-te Zufallsbit wird erzeugt, indem zunächst
xi = xi − 12 mod n
berechnet wird; von diesem Wert wird nur das niederwertigste Bit verwendet (das ist äquivalent zu einer Modulo-2-Operation; das niederwertigste Bit von 7 ist 1, da 7 mod 2 = 1). Der Vorteil dieses Generators ist, dass man das i-te Bit direkt berechnen kann, ohne die vorherigen i − 1 Bits zu kennen:
xi = x02i mod ((p − 1)(q − 1))
Aus diesem Grund eignet sich der BBS-Generator gut für Dateien mit wahlfreiem Zugriff.
Warum ist dieses Verfahren sicher? Der BBS-Generator setzt auf die Schwierigkeit der Faktorisierung von n. Dieser Wert selbst kann öffentlich bekannt sein, ohne Kenntnis der Faktoren p und q jedoch ist es nicht möglich, die Ausgabe des Generators vorherzusagen. Dank dieser Eigenschaft kann ein Kryptoanalytiker weder das vorhergehende noch das nächste Bit der Folge berechnen.
Das Ganze hat aber leider auch einen Nachteil: Der Algorithmus ist langsam. Zwar hat sich herausgestellt, dass man mehr als nur das niederwertigste Bit von xi verwenden kann (nämlich log2n Bits, wobei n die Länge von xi ist), trotzdem ist der BBS-Generator weiterhin vergleichsweise langsam und bleibt hinter schnellen Stromchiffrierungen wie RC4 weit zurück. Anwendungen mit hohen Sicherheitsanforderungen sollten jedoch auf diesen Generator keinesfalls verzichten, um z. B. sichere Schlüssel zu berechnen.
Mehr über Primzahlen, Faktorisierung etc. erfahren Sie im Kapitel über RSA.
Natürlich gibt es noch andere Zufallsgeneratoren, die ich hier jedoch nicht in langer Breite erklären möchte. Ich möchte Ihnen stattdessen einen Zufallsgenerator kurz vorstellen, der auf Basis verschiedener kryptographischer Algorithmen arbeitet – Yarrow. Das Prinzip ist schnell zu erklären: Um Zufallszahlen zu erzeugen, wird Triple-DES, d. h. dreifaches DES eingesetzt. Als Seed können bestimmte, sich schnell ändernde Werte fungieren (Systemauslastung, Bildschirminhalt, Systemzeit, Position des Mauszeigers, Aktionen des Benutzers usw.). Bevor der Seed-Wert als Schlüssel eingesetzt wird, wird er jedoch mit einer Einweg-Hashfunktion namens SHA-1 gehasht. Mit dem erhaltenen 160-Bit-Wert wird Triple-DES nun initialisiert. Der Counter kann auf einen beliebigen Wert gesetzt werden. Um die erste Zufallszahl zu erzeugen, verschlüsselt man den (wohlgemerkt 64 Bit-) Counter. So in etwa sieht das Grundprinzip von Yarrow aus. Wenn Sie mehr darüber erfahren möchten, schauen Sie mal bei Counterpane rein (in Englisch). Der Algorithmus wurde übrigens u. a. von Bruce Schneier entworfen.
In der Kryptographie sind PRNGs von großer Bedeutung. Allerdings finden Zufallsgeneratoren z. B. auch bei Spielen Verwendung, wobei es sich dabei jedoch um einfache und schnelle Algorithmen (z. B. lineare Kongruenzgeneratoren) handelt. Kryptographisch sichere Zufallszahlen benötigt man u. a. für
um einige Beispiele zu nennen. Für die Bewertung der Sicherheit eines PRNGs gelten ähnliche Kriterien wie für die Bewertung eines kryptographischen Algorithmus.
| nach oben |
Weiter |
Letzte Änderung: 24.03.2002
© 2002 by Christian Thöing