1Grundlagen

1.1Einführung

1.1.1Einleitung

Sicherheit : warum ?

Die Fähigkeiten von Computern haben sich sehr schnell entwickelt. Die technischen Möglichkeiten bieten umfangreiche Möglichkeiten, Informationen in hoher Geschwindigkeit auszutauschen. Die technische Stabilität von Verbindungen über tausende von Kilometern ist weitgehend gewährleistet, die Entwickler der logischen Transportmechanismen ( Protokolle ) hatten diese Aufgabe als Ausgangspunkt. Mit TCP ist ihnen ein Protokoll gelungen, das die zugesicherte und vollständige Übertragung auch von großen Datenmengen ermöglicht.
Das e-mail-System ist weltweit etabliert und aufgrund seiner einfachen Handhabung sehr beliebt und verbreitet. Darauf hatten die Entwickler auch größten Wert gelegt.
Der Datentransfer läuft zuverlässig, jedoch wurde bei der Implementation der Techniken nicht in Erwägung gezogen, daß die Daten auf ihrer Reise durch das Netz abgefangen und mißbraucht werden könnten. Dieser Aspekt trat erst in den Blickpunkt allgemeinen Interesses, als die Kommerzialisierung der Computertechnik durch das Internet einen Stand erreicht hatte, wo es möglich war, Geschäfte über übers Netz zu tätigen. Die Abwicklung eines Geschäftes erfordert von zumindest einer Seite die Preisgabe persönlicher Informationen. Der Geldverkehr setzt voraus, daß die Daten nicht abgefangen werden, ein Vertrauensverhältnis könnte sonst nicht entstehen.
Im privaten Sektor wie auch im wirtschaftlichen un wissenschaftlichen Bereich ist die Übertragung von vertraulichen Daten an der Tagesordnung. Diese Übermittlung gesichert über das Netz zu realisieren, stellt eine weitere Anforderung an die Entwickler.

Mechanismen zur geschützten Datenübertragung waren in den nicht Aufgabe der ursprünglichen Techniken und wurden so erst im Laufe der Zeit, als Reaktion auf ein gewachsenes Sicherheitsbedürfnis implementiert. Die Entwicklung von Sicherheitsmechanismen hat mit der Verbreitung der Computertechnik und der rasanten Entwicklung ihrer Möglichkeiten nicht standgehalten.

Die sichersten OS sind mit einer dedizierten Rechtevergabe ausgestattet. Die Verwaltung obliegt i.A. einem Systemverwalter. Seine Vertrauenswürdigkeit vorausgesetzt muß gewährleistet sein, daß zentrale und sicherheitsrelevante Daten nicht mit fehlerhaften Rechten versehen sind. Auch müssen die vielen Umwege bedacht werden, auf denen man (gezielt oder ungewollt) das Rechteschema kompromittieren kann.

Somit erfordert die Absicherung der Datenübertragung zunächst einmal die Absicherung der Systeme, von denen und zu denen Daten transferiert werden ( lokale Sicherheit ).
Dann muß die Sicherheit beim Transport über das Netz gewährleistet werden ( netzweite Sicherheit ).

Beide Anforderungen sind in letzter Konsquenz nicht zu erfüllen. Man kann aber die Möglichkeiten der Manipulation eines Datentransfers weitgehend einschränken, wenn man die Techniken der Angreifer und die Risiken der Transportmechanismen kennt.

Wo besteht ein Interesse, Daten abzufangen ?

• Wirtschaftsspionage

• Privates Auskundschaften

• Forscherdrang von Newcomern

• Staatliche Überwachung

Die Motive können sich sehr wohl überschneiden.

1.1.2Zielsetzung

Wir erzielen Sicherheit, indem wir einen Angriff so teuer machen,
daß die Kosten den Nutzen übersteigen.¹

Vertraulichkeit

Sender und Empfänger wollen sich darauf verlassen, daß niemand außer Ihnen in der Lage ist, die Nachricht zu lesen. Auch dann nicht, wenn ein Dritter dasselbe Chiffrierverfahren verwendet, jedoch nicht den Schlüssel.
Ziel ist die Vertraulichkeit der Nachricht.
Erreicht wird dieses Ziel mit der symmetrischen Verschlüsselung.

Authentizität

Sender und Empfänger wollen sich darauf verlassen, daß die Nachricht auch tatsächlich vom Sender kommt.
Ziel ist die Authentizität der Nachricht.
Erreicht wird dieses Ziel mit der asymmetrischen Verschlüsselung.

Integrität

Sender und Empfänger wollen sich darauf verlassen, daß die Nachricht bei der Übermittlung nicht verändert werden.
Ziel ist die Integrität der Nachricht.
Erreicht wird dieses Ziel mit Hashfunktionen ( Message-Digest, Fingerprint )

¹ : zitiert nach [IK]

1.1.3Klassifizierung von Kryptoverfahren

Symmetrische Verfahren : private key

Zur Verschlüsselung und zur Entschlüsselung wird derselbe Schlüssel verwendet.
Symmetrische Verfahren können in verschiedenen Modi angewandt werden.

Blockchiffre

Der Plaintext wird in Blöcke aufgeteilt.

Stromchiffre

Der Plaintext wird Byte- oder Bitweise verschlüsselt.

DES, 3DES, IDEA, Rijndael, Blowfish, Twofish, CAST5, RC2, RC4, RC5, RC6
( Skipjack, MISTY, E2, MARS, DEAL, SAFER+, LOKI, Crypton, DFC, FROG, Serpent, Hasty Pudding Cipher HPC, Magenta )

Modi : ECB, CBC, OFB, CFB

Asymmetrische Verfahren : public key

Zur Verschlüsselung und zur Entschlüsselung werden unterschiedliche Schlüssel verwendet.

RSA, DSA, El-Gamal

Hash - Funktionen

Hash-Funktionen ermitteln aus einem Plaintext einen Wert, der die Integrität der Daten gewährleistet. Aus dem Hashwert kann nicht auf den Inhalt der Daten geschlossen werden. Sie werden für Signaturen verwendet.

MD4, MD5, SHA, SHA-1, RIPEMD160

---

Getrennt von diesen Verfahren sind die Standards zur Datenaufbereitung zu betrachten.

PKCS#1 - PKCS#15, P1363

1.1.4Verfahren der Kryptographie

Diese Seite enthält die Beschreibung einiger z.T. historischer Verfahren der Verschlüsselung.

Monoalphabetische Verfahren

beruht auf der einfachen Verschiebung aller Buchstaben um einen bestimmten Wert innerhalb eines Alphabets. So wird z.B. der Buchstabe "A" durch verschieben um 5 Stellen im Alphabet zum "E", "B" wird zu "F" etc. Auch das Umdrehen des Alphabets und Zuordnung von "A" zu "Z", "B" zu "Y" etc. gehört in diese Kategorie der einfachsten Verschlüsselungsverfahren. Das ursprüngliche Alphabet wurde einfach in ein anderes transformiert, daher resultiert die Bezeichnung dieses Verfahrens.

Transpositions-Chiffre

basieren auf der Idee, die Reihenfolge von Buchstaben zu vertauschen. Z.B. wird dies erreicht, indem man den zu verschlüsselnden Text in Zeilen bestimmter Länge aufschreibt und dann vertikal liest. Dem Empfänger muß dann die ursprüngliche Zeilenlänge bekannt sein, um den Text zu dechiffrieren. Eine Information, die Auskunft über die Art der Dechiffrierung gibt, wird allgemein als Schlüssel bezeichnet.

Substitutions-Chiffre

Die Idee basiert auf dem monoalphabetischen Verfahren. Die Buchstaben werden ersetzt und behalten die Reihenfolge bei. Jedoch kann statt des Alphabets auch eine andere Symbolfolge ( z.B. Zahlen ) verwendet werden.
Nachteil : die statistische Buchstabenhäufigkeit bleibt erhalten.

Polyalphabetische Substitution

werden einzelne Buchstaben im Verhältnis zu ihrer relativen Häufigkeit im Text durch mehrere Buchstaben ersetzt. Die Methode konnte aber aus Gründen der Eindeutigkeit bei der Dechiffrierung nicht nur mit Buchstaben realisiert werden.

Vernam-Verfahren

Hierbei wird die Bitkette des Klartextes mit einem langen Schlüssel Bitweise XOR-verknüpft (bitweise Addition ohne Übertrag, eXclusive OR). Der Schlüssel wird wiederholt angewendet, wenn der Klartext länger als der Schlüssel ist.
Durch die wiederholte Anwendung des Schlüssels können durch Korrelation zweier verschlüsselter Nachrichten Informationen über den Schlüssel abgeleitet werden.
Eine erhebliche Verbesserung gewinnt man dadurch, daß der Schlüssel sich fortlaufend ändert ( s. One-Time-Pad ).

Vigenère-Verfahren

Es werden mehrere transformierte Alphabete erzeugt. Die zu verschlüsselnden Buchstaben werden jetzt mit den unterschiedlichen Transformationen verschlüsselt. Welcher Buchstabe in einem Wort mit welcher Transformation behandelt wird, kann zum Beispiel mit der Position des Buchstaben in einem Wort festgelegt werden. Hier werden also verschiedene Methoden nacheinander angewandt. Die Reihenfolge der Methoden ist der Schlüssel.
Der Nachteil der Buchstabenhäufigkeit taucht hier nicht auf, da gleiche Buchstaben des Klartextes jeweils durch verschiedene Buchstaben substituiert werden.
Blaise de Vigenère, 1523-1596, frz. Diplomat

One-Time-Pad

Beim One-Time-Pad wird der Klartext wie bei der Vernam-Chiffrierung bitweise mit einem Schlüssel verknüpft. Jedoch ändert sich der Schlüssel bei jedem Bit.
Wichtig ist hier, daß sich der Schlüsselstrom nicht wiederholt. Dazu muß eine echte Zufälligkeit des Schlüssels gewährleistet sein.
Wenn kein Zeichen des Klartextes mit derselben Verschlüsselungsmethode bearbeitet wird, ist die Rekonstruktion außerordentlich schwierig. Man erreicht dies in jedem Fall, wenn der Schlüssel ungefähr so lang ist wie der zu verschlüsselnde Text. Das ist der auch der entscheidende Nachteil, das Verfahren ist unhandlich : die Schlüssel müssen erzeugt und verteilt werden.
Die Vereinbarung eines Schlüssels großer Länge ( z.B. ein Buch ) führt auf das monoalphabetische Verfahren zurück.

1.2Symmetrische Verschlüsselung

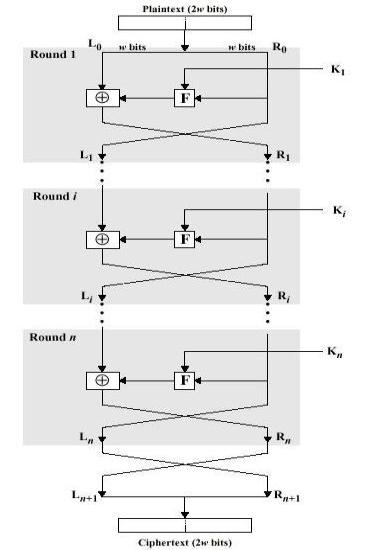
1.2.1Feistel

Horst Feistel entwickelte 1973 ein Schema zur Verschlüsselung, das für beinahe alle Blockverschlüsselungsverfahren angewendet wird.

Das Schema wird nach Stallings geschildert ([STA1] p. 44)

Notwendig sind also

1. Ein Schlüssel K₀

2. Ein Algorithmus zur Erzeugung von Unterschlüsseln

3. Eine Rundenfunktion F

4. Eine Implementation (Hard-/Software) zur Realisierung des Ablaufs.

Die Anzahl der Runden erhöht die Sicherheit, aber auch die Rechenzeit.

1.2.2DES

Geschichte

1973 initierte das amerikanische National Bureau of Standards (NBS) die Entwicklung eines Verschlüsselungsverfahrens zur allgemeinen Verwendung. IBM's Vorschlag "DES" wurde angenommen und 1977 vom NIST (eh. NBS, National Instute for Standards an Technology) als Standard anerkannt.

Beschreibung

DES ist ein symmetrisches Verschlüsselungsverfahren, das Daten blockweise verarbeitet ( Blockchiffre ). Die 8 Byte ( = 64 Bit ) großen Blöcke werden mit einem 8 Byte großen Schlüssel verschlüsselt. Von diesem 64-Bit Schlüssel werden 8 Bit zur Prüfsummenbildung verwendet. Somit arbeitet DES effektiv mit einer 56-Bit Verschlüsselung.
Eine genaue Beschreibung des Data Encryption Standard liefert die Federal Processing Standards Publication 46-2 .
DES ist "...ein mathematischer Algorithmus zur Verschlüsselung (Chiffrierung) und zur Entschlüsselung (Dechiffrierung) von binärcodierten Informationen. Beim Verschlüsseln werden die Daten in eine unverständliche Form gebracht, den Zifferncode. Beim Entschlüsseln dieses Zifferncodes werden die Daten wieder in ihre ursprüngliche Form gebracht, den sogenannten Klartext." [LHG]

Algorithmus

DES ist ein blockweises Verschlüsselungsverfahren, die Daten werden in 64bit-Blöcken behandelt.
Das Verfahren basiert auf dem Feistel-Algorithmus.
Dabei erfolgt auf den ersten Block eine erste Permutation (Datenbits werden reorganisiert), ein Eingabeblock wird erzeugt.
Die mathematische Transformation erfolgt wie bei Feistel.
Das Ergebnis der Transormation wird einer zweiten Permutation unterzogen. Das Ergebnis ist der verschlüsselte Text (Chiffretext).

Die Rundenfunktion F ( s. Feistel ) charakterisiert das Verfahren. Die permutierte Eingabe wird von 32 auf 48 Bit erweitert und mit 48 Bit des Schlüssels verknüpft (XOR). Anschließend erfolgt eine Aufteilung des 48-Bit Blocks in 8 Blöcke zu 6 Bit.
Je 6 Bit werden einer Substitutionsfunktion unterworfen ( S-Box ), deren Ergebnis 4 Bit lang ist. Für jeden der 8 6-Bit Blöcke existiert eine S-Box.

Eigenschaften

1. Symmetrisches Verfahren

2. Blockchiffre

3. 56-Bit Schlüssellänge

4. Verwendung von S-Boxen

5. Chiffretext und Plaintext haben gleiche Länge

1.2.3Blockchiffre : Modi

Bei symmetrischen Verschlüsselungsverfahren wie z.B. DES oder IDEA werden die Daten in 8 Byte großen Blöcken verschlüsselt.
Daher bezeichnet man solche Verfahren als Blockchiffre.

ECB : Electronic Codebook Mode

Jeder Block wird einzeln mit demselben Verfahren verschlüsselt.
Die Integrität der Daten ist nicht gewährleistet. Es können einzelne Blöcke herausgenommen oder Blöcke vertauscht werden.
Gleiche Blöcke werden stets gleich verschlüsselt.
Das kann einen Rückschluß auf den Inhalt ermöglichen.

CBC : Cipher Block Chaining

Jeder Plaintext-Block wird mit dem vorhergehenden Chiffre-Block verknüpft (XOR).
Dadurch werden gleiche Blöcke nicht mehr gleich verschlüsselt (wie beim ECB).
Damit der erste Plaintext-Block auch verknüpft werden werden kann, wird ein beliebiger Block an den Anfang des Verfahrens gesetzt.
Dieser beliebige Block heißt IV : Initialisierungsvektor.
Der IV braucht nicht geheim gehalten werden.

Parameter : IV

OFB : Output Feedback Mode ( Autokey )

Ein IV wird verschlüsselt. Das Ergebnis wird

a) mit einem Plaintext-Block verknüpft ( XOR ) und liefert den Chiffretext-Block.
b) verschlüsselt, das Ergebnis wird an den nächsten Vorgang weitergereicht

Der Schlüssel verändert sich nach jedem Verschlüsselungsvorgang.
Die Veränderung richtet sich nach der Ausgabe des Vorgangs.
Die Anzahl der Bytes für die Plaintext-Blöcke ( b ) ist nicht mehr festgelegt.

Parameter : IV, b ( <= 8 )

CFB : Cipher Feedback Mode ( Ciphertext Autokey CTAK )

Ein Chiffretextblock wird verschlüsselt, das Ergebnis wird mit dem nächsten Plaintext-Block verknüpft ( XOR ).
Die Blücke müssen genau wie beim OFB nicht 8 Byte groß sein .

Parameter : IV, b ( <= 8 )

1.3Asymmetrische Verschlüsselung

1.3.1RSA

RSA

RSA kann Daten verschlüsseln. Jedoch wird nur der symmetrische Sitzungsschlüssel verschlüsselt, da RSA langsamer als symmetrische Verfahren arbeitet.
Nicht die Daten, sondern der Sitzungsschlüssel wird verschlüsselt.
Die mit dem symmetrischen Schlüssel verschlüsselten Daten werden zusammen mit dem durch RSA verschlüsselten symmetrischen Schlüssel übertragen. Der verschlüsselte Schlüssel dient als digitaler Umschlag (digital evelope).
Das Verfahren :

Message - Receiver = Publickey - Sender		Message - Sender = Publickey - Receiver
wähle 2 Primzahlen p und q
berechne n= p * q (den Modulus)
berechne f(n) = (p-1)*(q-1)
vernichte p und q
wähle e (öffentlicher Exponent), teilerfremd zu f(n)		Nachricht m liegt in plaintext vor
n, e sind öffentliche Werte (public key)	n, e werden gesendet--------->	public key (n, e) wird gespeichert
berechne d = e-1 mod f(n)1 (private key)		berechne c = me mod n
d wird nie veröffentlicht		c ist der chiffretext
chiffretext wird empfangen	<----------------c wird gesendet
berechne cd = (me)d = me*d = m
m ist die gesendete Nachricht

,¹d.h. Welche Zahl mit e multipliziert modulo f(n) liefert 1 ? Dazu kann man vielfache von e bilden und mit 1 addieren.
Ist das Ergebnis durch e teilbar, so kann es als private key verwendet werden.=> Empfänger public key = (n,e) , private key = d

Sicherheit : Um einen privaten Schlüssel aus den öffentlich bekannten Werten (n,e) zu erhalten, muß f(n) bzw. p und q nachgebildet werden. Kurz : n muß in Primzahlen faktorisiert werden.
Deswegen werden beide Primzahlen etwa gleich groß gewählt (2*512 Bit = 1024 Bit)
Beispiel :
E : Zwei Primzahlen p = 3, q = 5 => n = p*q = 3*5 = 15
E : f(n) = (p-1)*(q-1) = 2*4 = 8
E : wähle e teilerfremd zu f(n), e= 11
E : Ermittle den private key d:

d = e^-1 mod f(n), dazu :
Berechne Vielfache von f(n), addiere 1 und teile sie durch e:
1*8+1 = 9 (nicht durch e=11 teilbar)
2*8+1 =17 (nicht durch e=11 teilbar)
3*8+1 =25 (nicht durch e=11 teilbar)
4*8+1 =33 (33 / 11 = 3) => d = 3

E : sende public key (n,e)=(15,11) an Sender.
S : Verschlüssele Nachricht m mit c = m^e mod n ( z.B. m = 3 )
S : sende c = m^e mod n = 3¹¹ mod 15 = 12 an E
E : Entschlüssele c = 12 mit c^d mod n = 12³ mod 15 = 3 (=m)

Die Technik von RSA basiert auf der Faktorisierung.

1.3.2Diffie Hellmann

DH Diffie-Hellman

Mit DH wird nicht verschlüsselt. Mit dem DH-Verfahren werden Schlüssel erzeugt. Beide Partner erzeugen dabei denselben symmetrischen Schlüssel.
Der Sender hat einen public value und einen private value.
Der Empfänger hat einen private value.
Der Sender schickt seinen public value an den Empfänger.
Mit dem public value errechnet der Empfänger seinen public value.
Der Empfänger schickt seinen public value an den Sender.
Beide können jetzt mit ihren value-pairs denselben symmetrischen Schlüssel generieren.

Sender		Empfänger
wähle 2 Primzahlen p = 7 und q = 5
besitzt y = 2 ( private value )		besitzt x = 5 (private value)
berechne public value ps = qy mod p =4
sende q,p,ps	q=5 p=7 ps=4 --------->	berechne public value pe = qx mod p = 3
	<------- pe=3	sende public value
berechne key=(pe)y mod p		berechne key=(ps)x mod p
key = 3 2 mod 7 = 9 mod 7 = 2		key = 4 5 mod 7 = 2
Verschlüssele mit key		Entschlüssele mit key

Sicherheit : Um den Schlüssel mit den public values (g,p und ps oder pe) zu erzeugen, muß ein private value bekannt sein.
Die Gleichung ps = g^z mod p muß nach z aufgelöst werden.
Im Bereich der Reellen Zahlen ( ps = g^z ) führt das auf den bekannten Logarithmus.
Durch den Modulooperator führt das auf den diskreten Logarithmus, der nur mit erheblichen Aufwand zu lösen ist, wenn die Primzahl p groß gewählt wird.
Die Technik von DH basiert auf dem diskreten Logarithmus.

1.4Signaturen

1.4.1Signaturen und Zertifikate

Vertrauen ist gut, Kontrolle ist besser. (Wladimir I. Uljanow)

Signaturen

Bei den asymmetrischen Verfahren ist die Vertraulichkeit der Daten gewährleistet. Der öffentliche Schlüssel kann zur Verschlüsselung verwendet werden.
Allerdings ist die Authentizität und Integrität des öffentlichen Schlüssels einer Person nicht gewährleistet.
Der Verteiler des public keys kann auf diesen Schlüssel eine Hash-Funktion anwenden und das Ergebnis ( fingerprint ) sowie die Bezeichnung der Hash-Funktion dem public key beifügen.
Nun kann dieser erweiterte public key geprüft werden : der Empfänger wendet auf den public key die angegebene Hash-Funktion an und vergleicht das Ergebnis mit dem Hashwert des Empfängers.
Stimmen beide Werte überein, so ist die Integrität des public keys gewährleistet.
Um jetzt noch die Authentizitä zu gewährleisten, wird der Hashwert vom Verteiler mit seinem private key entschlüsselt ( ! ). Der Empfänger kann mit dem public key diesen Wert verschlüsseln und hat den originalen Hashwert.
Der Fingerprint kann öffentlich gemacht werden, er nutzt ausschließlich dem Empfänger des public keys und niemanden sonst.

Dieses Verfahren ist nicht auf einen public key beschränkt, es kann auch auf normale Daten angewendet werden und dient dann als digitale Unterschrift ( Signatur ).

Zertifikate

Wurde ein public key vom Empfänger überprüft, so wird dem public key eine Prüfbestätigung beigefügt ( Zertifikat ).

Vertrauen

Public keys müssen nicht vom ursprünglichen Besitzer verteilt werden.
Wird ein public key von einer dritten Partei verteilt, so stellt sich die Frage, ob man dieser Partei vertrauen kann.

Alice besitzt public key von Charly ( third party )
Charly besitzt public key von Bob
Charly sendet public key von Bob an Alice

Kann Alice den public key von Bob bedenkenlos verwenden ? Ja, wenn Sie Charly vertraut.
Dazu kann Sie dem public key von Charly eine Eigenschaft beigeben, ob von Charly übermittelte public keys's direkt verwendet werden können ( ohne daß Alice diese zertifiziert ).
Die Vergabe einer solchen Eigenschaft führt dazu, daß jeder public key diese Eigenschaft besitzen muß, sogar der eigene public key von Alice.
Alice kann Charly also vertrauen, dann gibt sie dem public key von Charly eine Eigenschaft "Immer Vertrauen".
Oder Alice vertraut Charly nicht, dann gibt sie dem public key von Charly eine Eigenschaft "Nie Vertrauen".
Durch eine solche Verteilung von trusted peers entsteht ein sogenanntes web of trust, eine nicht hierarchische Struktur der Vertrauensstellungen ( PGP arbeitet mit einem web of trust ).
Ein web of trust ist mit steigender Teilnehmerzahl allerdings unübersichtlich.

Datenaufbereitung

Dem reinen public key werden vor der Übermittlung also noch Daten beigefügt :
Der Name des verwendeten Verschlüsselungsverfahrens,
Ein Hashwert ( fingerprint ),
der Name der Hash-Funktion,
das (die) Zertifikat(e) des ursprünglichen Besitzers und anderer Verteiler.
In welcher Form diese Daten übermittelt werden, damit sie vom Empfänger auch ausgewertet werden können, legen diverse Standards fest ( insbesondere PKCS#1 von RSA ).

2PGP Web of Trust

2.1Allgemeines

2.2Schlüsselerzeugung

Erzeugung eines Schlüsselpaares

pgp -kg

führt zu einem Dialog, in dem folgende Informationen gefragt werden:

1. RSA -Schlüssellänge
   in Bytes (384 - 8192)
2. Personal ID oder auch UserID
   Syntax :

   Mein Name (Kommentar) <mail> (Optionen)

   Die Mailadresse scheint bei der Verwendung von PGP in Mailclients wesentlich zu sein.
3. Passphrase
   Der private key wird mit einem Hashwert auf die passphrase abgespeichert. Dadurch ist der Zugang zum private key nur über die passphrase möglich.
4. Tastatureingaben
   Dient zur Erzeugung echter Zufallswerte bei der Schlüsselerzeugung.
   Gemessen werden die Zeitintervalle zwischen den Tastatureingaben.

Es werden Dateien in $PGPPATH erzeugt ( ~/.pgp/ ) :

• secring.pgp
  Enthält den private key ( incl. hash(passphrase) und UserID)
• pubring.pgp
  Enthält den public key mit der UserID. Diese Datei kann public keys anderer Personen aufnehmen.
• randseed.bin

Informationen über Schlüsselinhalte

pgp -kv <keyring_file>
Es existieren mindestens zwei Dateien : Eine für die private keys, eine für die public keys.
Die Ansicht der Dateien mit dem Kommando pgp -kv liefert für

• private keys

  Key ring: 'secring.pgp'
  Type Bits/KeyID    Date       User ID
  sec  1024/F9911C4F 2002/06/13 willy <willy@willy.bald.com>

• public keys

  Key ring: '/home/michi/.pgp/pubring.pgp'
  Type Bits/KeyID    Date       User ID
  pub  1024/F9911C4F 2002/06/13 willy <willy@willy.bald.com>
  sig       F9911C4F             willy <willy@willy.bald.com>

2.3Signaturen

Was ist eine Signatur ?

Eine Signatur ist ein mit dem privatekey ent-(!)schlüsselter Digest.
Ein Digest ist eine Zahl, die mit einer bestimmten (Hash)-Funktion aus den Daten (z.B. einer Datei ) ermittelt wird. Aus dieser Zahl (Hashwert, Fingerprint) sind die ursprunglichen Daten nicht reproduzierbar. Der Digest einer Datei ist weitgehend eindeutig, d.h., es gibt (fast) keine zwei Dateien unterschiedlichen Inhalts mit demselben Hashwert.
Theoretisch ist der Fall möglich, da der Hashwert eine beschränkte Länge hat (z.B. 128 bit), es gibt aber mehr als 2 hoch 128 mögliche Dateien. Man spricht dann von einer Kollision.
Der bekannteste Hashalgorithmus ist der MD5 (Message Digest No. 5, 128 bit).
Weite Verbreitung hat auch der SHA1 (Secure Hash Algorithmus Version 1, 168 bit) gefunden.
Darüber hinaus ist der RipeMD160 bekannt.
PGP verwendet den MD5.

Signatur erstellen pgp -s

pgp -sat <file_name>
Erstellt eine Datei names file_name.asc
Beispiel : Bob hat einen privatekey und eine Datei secr_mail
bob@thin1:~> pgp -sat secr_mail
bob@thin1:~> cat secr_mail.asc

-----BEGIN PGP SIGNED MESSAGE-----
babs@reeperbahn.de
susi@franktfurt.com
-----BEGIN PGP SIGNATURE-----
Version: 2.6.3in
Charset: noconv
iQCVAwUBPZw4zW0b1JBWNwO/AQEaWQQAg0u1aTh94TpuG4gt609UCe9TvLKlfhcF
... =lg7W
-----END PGP SIGNATURE-----

Achtung : Der Dateiinhalt wurde nicht verschlüsselt. der Digest wurde verschlüsselt und BASE64 codiert (Schalter a)
Bei Verwendung von -t bleibt der Dateiinhalt im Klartext, ohne -t wird der Dateiinhalt ebenfalls BASE64-codiert.
Die BASE64-kodierung wird insbesondere im Internet verwendet.

Signatur überprüfen

PGP erkennt am Inhalt einer Datei, ob sie signiert wurde.
Daher genügt Alice der publickey von Bob (pgp -ka pub_bob.pgp) und die secr_mail.asc - Datei :

alice@thin1:~> pgp secr_mail.asc
File has signature.  Public key is required to check signature.

Good signature from user "bob".
Signature made 2002/10/03 13:00 GMT using 1024-bit key, key ID 563703BF
Plaintext filename: secr_mail

Signatur seperat

pgp -sb <file_name>
erstellt eine Datei file_name.sig, in der nur die Signatur vorhanden ist.

Bemerkung

Der Hashwert einer Datei kann mit PGP-mitteln nicht sichtbar gemacht werden.
Das geht nur bei Hashwerten von publickeys (pgp -kvc).

2.4Trustmodell : Web of Trust

Das PGP Vertrauensmodell basiert auf

1. Validity
   Ein public key einer Person kann in einen keyring aufgenommen werden ( pgp -ka )
   Dabei kann dieser public key signiert werden. Mit der Signatur unterzeichnet man die Authentizität des public keys (dieser public key gehört zu der Person mit der UserID).

2. Trust
   Einem public key einer Person kann ein trustlevel mitgegeben werden.
   Damit kann geregelt werden, wie mit weiteren public keys verfahren wird.
   Beispiel : Alice Bob und Charly.
   Alice hält Bobs public key. Bob hält Charlys public key und hat ihn signiert.
   Alice erhält nun Charlys public key, der von Bob signiert wurde.
   Alice kann nun entscheiden :
   Entweder signiert sie selbst Charlys public key
   oder sie nimmt ihn in ihren public keyring auf, weil sie Bob vertraut.
   
   Ob sie Bob vertraut ( für diesen Zweck ) legt sie im trustlevel von Bobs public key fest.
   Das geschieht in dem Moment wo sie Bobs public key in ihren public keyring aufnimmt.
   Es gibt derzeit vier trustlevel :

   1. trustlevel : Explizite Nachfrage bei Einführung eines public keys

   2. trustlevel : No trust

   3. trustlevel : Usually, ein bißchen wird vertraut.
      d.h. wenn Alice zwei public keys von Tim und Tom hält und mit dem trustlevel 3 belegt,
      dann muß ein neuer public key einer weiteren Person ( Susi ) von Tim und Tom signiert sein, damit er von Alice automatisch signiert wird.

   4. trustlevel : Always, immer wird vertraut

pgp -ka <pub_key_file> , der vollständige Dialog

One or more of the new keys are not fully certified.
Do you want to certify any of these keys yourself (y/N)? y

Key for user ID: Michael Kalinka 
1024-bit key, key ID E957DAAD, created 2002/06/12
Key fingerprint = B1 71 2E AD 3C 57 B1 D3  F3 66 BE D6 E5 36 00 CB
This key/userID association is not certified.
  Questionable certification from:
  Michael Kalinka <mkalinka@web.de>

Do you want to certify this key yourself (y/N)? y

Looking for key for user 'Michael Kalinka <mkalinka@web.de>':

Key for user ID: Michael Kalinka <mkalinka@web.de>
1024-bit key, key ID E957DAAD, created 2002/06/12
            Key fingerprint = B1 71 2E AD 3C 57 B1 D3  F3 66 BE D6 E5 36 00 CB


READ CAREFULLY:  Based on your own direct first-hand knowledge, are
you absolutely certain that you are prepared to solemnly certify that
the above public key actually belongs to the user specified by the
above user ID (y/N)? y


READ CAREFULLY:  How did you prove the users real identity ?
        0) What? I do not understand this question.
        1) No attempt made at all to identify the user with a real name.
        2) Some casual attempt made to identify user with his name.
        3) Heavy-duty identification efforts, photo ID, direct contact...
3

You need a pass phrase to unlock your RSA secret key.
Key for user ID: willy <willy@willy.bald.com>
1024-bit key, key ID F9911C4F, created 2002/06/13

Enter pass phrase: Pass phrase is good.  Just a moment....
Key signature certificate added.

Make a determination in your own mind whether this key actually
belongs to the person whom you think it belongs to, based on available
evidence.  If you think it does, then based on your estimate of
that person's integrity and competence in key management, answer
the following question:

Would you trust "Michael Kalinka <mkalinka@web.de>"
to act as an introducer and certify other people's public keys to you?
(1=I don't know. 2=No. 3=Usually. 4=Yes, always.) ?

2.5Schlüsselverwaltung

2.6Keyserver

2.7PGP Kommandos

pgp -h ( pgp Version 2.6.3 )

Here's a short summary of commands in PGP 2.6.3i:

Generate new key pair:  pgp -kg    [keybits] [ebits] [factor1] [factor2] [mask1] [mask2]
Add key:                pgp -ka     keyfile            [keyring]
Extract key:            pgp -kx[a]  userid   keyfile   [keyring]
View key(s):            pgp -kv[v] [userid]            [keyring]
View fingerprint:       pgp -kvc   [userid]            [keyring]
Check & view in detail: pgp -kc    [userid]            [keyring]
Remove userid or key:   pgp -kr     userid             [keyring]
                        (Repeat for multiple userids on a key)
Edit trust params:      pgp -ke     userid             [keyring]
Add another userid:     pgp -ke     your_userid        [keyring]
Edit passphrase:        pgp -ke     your_userid        [keyring]
Sign a key in pubring:  pgp -ks  other_id [-u sign_id] [keyring]
Remove a sig from key:  pgp -krs    userid             [keyring]
Revoke, dis/enable:     pgp -kd     userid             [keyring]
Revoke a certificate:   pgp -kds other_id [-u sign_id] [keyring]

Encrypt:                pgp -e[a]  textfile TO_id [TO_id2 TO_id3...]
Sign:                   pgp -s[a]  textfile                         [-u MY_id]
Sign & encrypt:         pgp -se[a] textfile TO_id [TO_id2 TO_id3...][-u MY_id]
Make detached cert:     pgp -sb[a] [+clearsig=on] mainfile          [-u MY_id]
  (Can do binaries)     (clearsig=on may be set in CONFIG.TXT)
Encrypt with IDEA only: pgp -c     textfile
Decrypt or check sig:   pgp [-d] [-p] cryptogram
                        (-d to keep pgp data, -p for original file name)
Check detached cert:    pgp certfile [mainfile]
                        (If root of filenames are the same omit [mainfile])

Use [a] for ASCII output
Use [-o outfile] to specify an output file
Use [-@ textfile] to specify additional userids when encrypting
Use [-z"pass phrase"] to specify your pass phrase
Use [+batchmode] for errorlevel returns
Use [f] for stream redirection ( pgp -f[ARGS] <infile >outfile )
Use [w] to wipe plaintext file (encryption operations)
Use [m] to force display of plaintext only (no output file)
Use [t] to alter line endings for unix, etc.

2.8PGP for Windows Installation

Die Software

Homepage http://www.pgpi.org
Lokal PGPFW703.zip ( 7.2 MB .zip ) aktuelle Version 7.0.3 ( Stand 17. Oktober 2002 )
für Windows 98/ME/2000
Die Hilfefunktion ersetzt jede Dokumentation.

Installation

Als Administrator das zip-Archiv entpacken und die PGP_FW/PGPfreeware 7.0.3.exe starten.
Es beginnt eine Standardinstallation unter Windows (Lizenz, Destination-Folder ... ).
Dann erscheinen die möglichen PlugIns. Für das Eudora-Plugin wird nach dem Inst-Pfad von Eudora gefragt.

Nach der installation

Grundlegende Informationen über die Konfiguration finden sich in
.../Administrator/Anwendungsdaten/Network Associates/PGP/PGPprefs.txt

2.9PGP for Windows Schlüsselerzeugung

User und Schlüsselpaare

Nach der Installation wird jedem User bei der Anmeldung angeboten, eine PGP-Schlüsselpaar zu erzeugen

Das Experts-Menu ermöglicht einem genaue Angaben zur Schlüsselerzeugung,
Für den Gebrauch des PGP-privatekeys wird eine Passphrase vereinbart

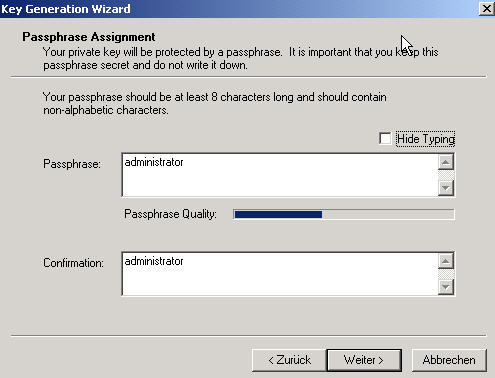
Die Erzeugung eines Schlüsselpaares ist damit abgeschlossen

2.10PGP for Windows Outlook Express

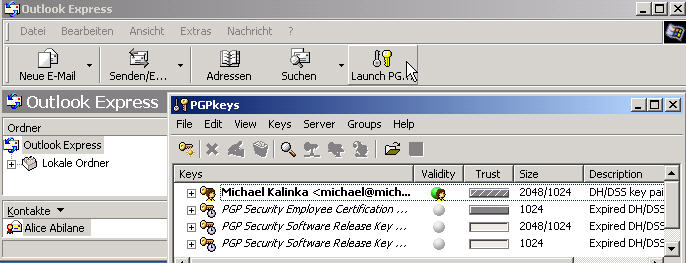
PGP-Schlüssel im Outlook Express

Im OE erscheint jetzt ein neuer Button : Launch PGPkeys. Im zugehörigen Fenster werden die öffentlichen Schlüssel im Keyring des Users angezeigt.
Die Schlüssel kjönnen von dort verwaltet werden (Import,Export und vieles mehr)

Im Menu Edit/Options/Email kann festgelegt werden, ob Mails mit PGP verschlüsselt werden sollen.
Dort wird auch festgelegt,wie verschlüsselte einkommende Mails bearbeitet werden sollen. ( und und und ...)

PGP-Schlüssel importieren

Neue öffentliche Schlüssel können nach dem folgenden Schaubild importiert werden.

Die publickeys können zum Beispiel in einer Datei vorliegen oder aber in einer Mail gesendet werden.
Es kann intuitiv gearbeitet werden, Für genaue Anleitungen sei auf die Hilfe verwiesen.

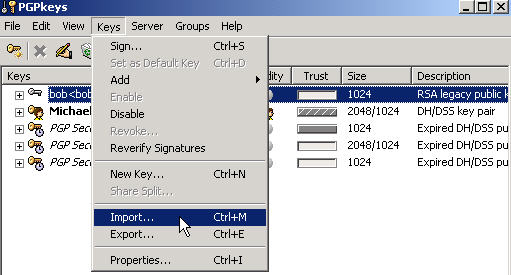
Allgemeiner Hinweis

Die PGP-Verschlüsselung verläuft vollkommen unabhängig von der MS-Zertifikatsverwaltung

3OpenSSL

3.1Engine

OpenSSL ist eine Sammlung von Programmen, die verschiedene Aufgaben erfüllen.
Download :OpenSSL 0.9.6h für Windows (5.1 MB .msi)
Original :ftp.runestig.com
Links : OpenSSL.org
Links : netzadmin.org

3.2Symmetrische Verschlüsselung

3.3Asymmetrische Verschlüsselung

3.3.1Private Schlüssel erzeugen

Erzeugung privater Schlüssel : openssl genrsa ( man genrsa )

Einfacher Schlüssel

genrsa erzeugt einen einfachen Schlüssel mit 512 Bit Länge.
Der Schlüssel kann in einer Datei ( -out ) gespeichert werden, die Länge ist variabel.
Beispiel :

openssl genrsa -out my_key_file.pem 1024

Die gewünschte Key-Länge ist immer das letzte Argument.
Der Inhalt der Datei lautet dann

-----BEGIN RSA PRIVATE KEY-----
MIIBOwIBAAJBAKr66O+KfQAGuRnWSQcjy92mM6jrvoX6vYzDe3l9NQy3HlCKuuDb
... 6Wa0J6+BYdAuzoJ5lG8U42D6ng2Ce7wV5K/eaB9lYA==
-----END RSA PRIVATE KEY-----

Der Inhalt des private keys kann detailliert dargestellt werden :

openssl rsa -in my_key_file.pem -noout -text
read RSA key
Private-Key: (1024 bit)
modulus:
    00:d6:09:d3:6c:00:86:0f:f4:2e:83:36:73:62:5f:
    85:27:3f:bb:0b:b6:73:45:4c:bf:36:82:1d:7d:ba:
    ...    d2:20:d9:94:2a:82:38:ba:b3
publicExponent: 65537 (0x10001)
privateExponent:
    00:ac:b6:23:0f:2c:61:01:70:a5:33:a5:f5:77:74:
    e2:8a:28:47:f3:8c:96:f9:5d:93:92:15:6e:5c:ac:
    ...    e8:05:67:a3:1d:b9:6c:a7:09
prime1:
    00:f6:6b:5d:51:77:d0:4e:e2:67:a7:de:f2:5c:1b:
    ...    70:43:40:8f:97
prime2:
    00:de:5c:2b:8a:fc:3b:ed:f1:df:ea:21:e4:c9:27:
    ...    b4:93:1f:11:45
exponent1:
    76:a4:a6:df:8c:b2:6c:e8:b1:43:b0:22:3c:9a:a2:
    ...    44:f5:16:ad
exponent2:
    00:8e:f4:c6:f1:c6:14:69:77:f5:b3:3b:33:31:b7:
    ...    a3:6d:6a:ad:d9
coefficient:
    00:f0:9e:3b:a2:3d:2d:86:2e:f1:ad:c9:9b:b8:00:
    ...    ad:9b:e5:da:5b
thin1:/usr/share/ssl #

Verschlüsselter Schlüssel

Ein privater Schlüssel kann seinerseits verschlüsselt werden, um die Verwendung des Schlüssels
von Kenntnis einer sog. Passphrase ( zuweilen auch Mantra genannt ) abhängig zu machen.
Der Schlüssel kann mit -des , -3des oder -idea verschlüsselt werden.
Beispiel :

openssl genrsa -des 1024
Son Jun  2 16:36:07 CEST 2002
Generating RSA private key, 1024 bit long modulus
..............++++++
......................++++++
e is 65537 (0x10001)
Enter PEM pass phrase:
Verifying password - Enter PEM pass phrase:
-----BEGIN RSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: DES-CBC,45A38664FB9FA569

f9XrzjbLynEJNcpFFyj9H9+dbUkIlBplE/UbMQ3/OOcDNtu62O3tIIKOX5aOtin8
...... dMS/L/xmFVrg5kHsXtzKzB9m/lwM+Ko06744cAGek/4NMwzCg==
-----END RSA PRIVATE KEY-----
Son Jun  2 16:36:19 CEST 2002

3.3.2Öffentliche Schlüssel erzeugen

Erzeugung öffentlicher Schlüssel : openssl rsa ( man rsa )

Öffentlicher Schlüssel aus dem Privaten Schlüssel

rsa erzeugt einen öffentlichen Schlüssel aus einem privaten Schlüssel ( -pubout ).
Der Schlüssel kann in einer Datei ( -out ) gespeichert werden, die Länge ist variabel.
Beispiel :

openssl rsa -pubout -in privkey_file.pem -out pubkey_file.pem

Der Inhalt der Datei lautet dann:

-----BEGIN PUBLIC KEY-----
MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAKr66O+KfQAGuRnWSQcjy92mM6jrvoX6
vYzDe3l9NQy3HlCKuuDbsc095tJwL47G6TXpK5XW5rtHgsQtOjWk628CAwEAAQ==
-----END PUBLIC KEY-----

Der Inhalt des public keys kann detailliert dargestellt werden ( -pubin ):

openssl rsa -pubin -in testpub.pem -noout -text
read RSA key
Modulus (512 bit):
    00:aa:fa:e8:ef:8a:7d:00:06:b9:19:d6:49:07:23:
    cb:dd:a6:33:a8:eb:be:85:fa:bd:8c:c3:7b:79:7d:
    35:0c:b7:1e:50:8a:ba:e0:db:b1:cd:3d:e6:d2:70:
    2f:8e:c6:e9:35:e9:2b:95:d6:e6:bb:47:82:c4:2d:
    3a:35:a4:eb:6f
Exponent: 65537 (0x10001)

Ersichtlich werden hier nur der Exponent und der Modulus als Produkt zweier Primzahlen gespeichert, nicht aber die einzelnen Primzahlen. Die Kenntnis des Modulus läßt jedoch keinen Rückschluß auf die verwendeten Primzahlen zu. Deren Kenntnis ist für die Erzeugung des private keys notwendig ( Faktorisierung ).

3.3.3Mechanismus der der Publickey-Verschlüsselung

Alice verschlüsselt Daten mit 128bit, symmetrisch (16Byte)

Gegeben : Datei plainfile.txt und 16Byte ("abcdabcdabcdabcd") als Symmetrischer Schlüssel
Verwendet : blowfish - Verschlüsselung im CBC-Mode ( -bf )

openssl enc -e -bf -k "abcdabcdabcdabcd" -in plainfile.txt -out cipherfile.xtx

Streng gesehen wird aus der Zeichenkette "abc..." erst ein 128-Schlüssel erzeugt.
Die Zeichenkette kann auch kürzer oder länger als 16 Byte sein.
Sie ist nicht der Schlüssel, wird aber wie ein Schlüssel verwendet.

Alice verschlüsselt den Symmetrischen Schlüssel mit Bobs publickey

Gegeben : Symmetrischer Schlüssel, 128 bit ( 16Byte), Bobs publickey bob_pub.pem

 openssl rsautl -encrypt -pubin -in plain.key -inkey testpub.pem -out crypt.key

-encrypt : es wird verschlüsselt
-pubin : es wird mit einem öffentlichen Schlüssel verschlüsselt (-inkey)
-in : enthält den sym. Schlüssel im Klartext (plain.key), STDIN-Eingabe möglich.

Alice sendet Daten und den verschlüsselten symmetrischen Schlüssel an Bob

Übermittelt werden Dateien cipherfile.xtx und crypt.key

Bob entschlüsselt den symmetrischen Schlüssel mit seinem privatekey

Gegeben : Verschlüsselter sym. Schlüssel (crypt.key) , Bobs privatekey

openssl rsautl -decrypt -in crypt.key -inkey bob_priv.pem -out plain.key

Der symmetrische Schlüssel liegt jetzt im Klartext in der Datei plain.key bei Bob

Bob entschlüsselt die Daten mit dem symmetrischen Schlüssel

Gegeben : Verschlüsselte Daten in Datei cipherfile.xtx, sym. Schlüssel in Datei plain.key

openssl enc -d -bf -kfile plain.key -in cipherfile.xtx -out plainfile.txt

Der Klartext liegt jetzt in der Datei plainfile.txt vor

Was übermittelt wird

1. Dateien :
   Die Datei cipherfile.xtx, die mit einem 128-bit Schlüssel symmetrisch Verschlüsselt wurde
   Die Datei crypt.key, die mit Bobs publickey verschlüsselt wurde und nur mit seinem privatekey entschlüsselt werden kann.
   Übermittelt werden
2. Informationen :
   Das Verschlüsselungsverfahren ( hier : Blowfish CBC )
   Die Schlüsselllänge ( es gibt Verfahren mit variabler Schlüssellänge z.B. AES-Rijndael )

Bemerkung

Der gezeigte Mechanismus beschränkt sich auf die Schlüsselübergabe.
Um die Integrität der Daten zu gewährleisten, kann ein Digest verwendet werden.
Um die Authentizität der Daten zu gewährleisten, kann Alices privatekey verwendet werden und ihr publickey muß Bob bekannt sein.

3.4Digests

3.5Zertifikate

3.5.1Verzeichnisstruktur und Initialisierung

Das Standardverzeichnis

Das Standardverzeichnis unter SuSE-Linux befindet sich unter /usr/share/ssl (=$CA_PATH), es kann aber beliebig gehalten werden. Dazu muß die openssl.cnf angepaßt werden.
Die Zugriffsrechte der Verzeichnisse richten sich nach der Art der Verwendung :
Administration auf Shellebene erfordert rwx-Rechte für den CA-Admin ( z.B. $user=root );
Administration auf CGIebene erfordert rwx-Rechte für den Webserver ( z.B. $group=nogroup)

Seriennummern : Datei serial

Jedes Zertifikat bekommt eine Seriennummer, die Bestandteil des Zertifikats ist. Die Datei serialenthält die aktuelle Seriennummer als hexadezimale Zahl. Beim Erstellen eines Zertifikates wird die Datei ausgelesen und der aktuelle Wert verwendet. Nach erfolgreichem Erstellen des Zertifikats wird der Inhalt um 1 erhöht.
Die Datei muß u.U. angelegt werden und mit der ersten Seriennummer belegt werden.
Beispiel : echo "00" > serial
Achtung : Nach Erstellen des RootCA-Zertifikats wird die serial nicht automatisch um 1 erhöht., die Datei muß editiert werden.

Datenbank : Datei index.txt

Zur Verwaltung aller Zertifikate wird eine Datenbank mit Informationen zu einem Zertifikat gehalten, die Datei index.txt. Der Schlüssel dieser Datenbank ist die Seriennummer.
Beispiel :

V       030919070528Z           00      unknown /C=DE/ST=S-H/O=MKCA/OU=MKCAunit/CN=MKalinka/Email=root@michi.de

Bedeutung der Einträge :
1. Spalte : V für valid, R für Revoked oder E für expired
2. Spalte : Endzeitpunkt der Gültigkeit im UTC-Format ( YYMMDDHHMMSSZ, GMT)
3. Spalte : Leer für valid certificates, sonst : revocationtime (UTC)
4. Spalte : Seriennummer
5. Spalte : Location des Zertifikats ( z.Zt. wird immer unknown verwendet )
6. Spalte : Distinguished Name des Antragstellers (Subject)

Als Datensatztrenner kann der Tabulator verwendet werden.

Achtung : Bei der Erstellung eines RootCA-Zertifikats wird ein Eintrag nicht automatisch erzeugt. Der Endzeitpunkt der Gültigkeit eines Zertifikats kann mit

openssl x509 -in <cert_file> -enddate -noout

ausgelesen werden und in das UTC-Format konvertiert werden.

3.5.2Konfigurationsdatei openssl.cnf

Die Konfigurationsdatei /usr/share/ssl/openssl.cnf regelt das Verhalten der openssl-Suite bei Anwendung spezieller Programme, die Certificate-Requests bearbeiten ( req, ca, (x509?)).
Die Datei besteht aus Abschnitten ( [ xyz ] ) und Variablen ( var_name ).
Variablen in Abschnitten können Abschnittsnamen enthalten, sie verweisen dann auf einen weiteren Abschnitt.

Eine CA erstellt und verwaltet Zertifikate und Certificate-Revocation-Lists (CRL).
Zu diesem Zweck muß sie eine bestimmte Infrastruktur erzeugen :

1. Verzeichnis für die Zertifikate

2. Datei mit aktueller Seriennummer
   Alle von einer CA ausgestellten Zertifikate bekommen eine ( für diese CA eindeutige )Seriennummer.

3. Verzeichnis für die CRLs

4. Datei mit Statusinfos für Zertifikate ( index.txt, database )

5. Datei/Verzeichnis für das CA-Zertifikat, CA-privatekey, CA-CRL

Diese Angaben werden in dem Abschnit [ ca ] definiert.
Die Regeln, nach denen Zertifikate erstellt werden dürfen

3.5.3Zertifikate allgemein

Zertifikate

Zertifikate beinhalten einen Publickey, der mit einem Digest versehen ist. Dieser publickey wird von einer dritten Instanz ( third party ) beglaubigt, d.h. mit dem private key der third party signiert und wiederum mit einem Digest versehen. Alle verwendeten Algorithmen müssen dann im Zertifikat übermittelt werden.

Inhalte eines Zertifikats ( X509 )

v1	v2	v3	Inhalt	Beispiel
x	x	x	Version	3 (0x2)
x	x	x	Serial Number	2 (0x2)
x	x	x	Signature-Algorithm	md5WithRSAEncryption
x	x	x	Issuer	C=DE, ST=SH, L=Kiel, O=MKCA, OU=mkcau, CN=MKalinka/Email=root@michi.de
x	x	x	Validity	Not Before: Oct 4 17:00:42 2002 GMT Not After : Oct 4 17:00:42 2003 GMT
x	x	x	Subject	C=DE, ST=SH, O=MKCA, OU=privates, CN=Alice Abilane/Email=alice@michi.de
x	x	x	Subject Public Key Info	Public Key Algorithm: rsaEncryption RSA Public Key: (1024 bit) Modulus (1024 bit): 00:b4:2a:0e:8b:9e:d3:9d:39:c4:7b:71:e5:7f:a1: c5:65:72:7f:f9:eb:73:74:10:ce:56:9f:96:56:18: ... dc:c0:93:11:39:3b:15:16:8d Exponent: 65537 (0x10001)
	x	x	eindeutiger Issuer Name	<optional>
	x	x	eindeutiger Subject Name	<optional>
		x	X509v3 extensions	X509v3 Basic Constraints: CA:FALSE Netscape Comment: OpenSSL Generated Certificate X509v3 Subject Key Identifier: 5F:3D:72:11:2D:6A:AF:BB:06:B7:08:E2:D4:89:7B:78:87:1E:C4:6D X509v3 Authority Key Identifier: keyid:17:00:4D:63:21:59:7B:96:CA:44:34:DE:47:89:71:D8:3F:CF:4E:B5 DirName:/C=DE/ST=SH/L=Kiel/O=MKCA/OU=mkcau/CN=MKalinka/ Email=root@michi.de serial:00
x	x	x	Signature Algorithm	md5WithRSAEncryption d9:a2:15:4e:6f:0f:d4:d9:22:c1:48:63:d9:d9:dc:9a:d2:c9: 0e:08:a6:90:08:76:63:57:b1:e8:ea:3c:17:34:e1:13:d2:c2: ... a2:f2

Erstellung eines Zertifikats

Erstellt eine CA (issuer) ein Zertifikat für einen Antragsteller (subject), so kann sie dem Z. eine Reihe von Parametern mitgeben und von dem subject die Erfüllung bestimmter Auflagen verlangen. Deswegen erstellt das subject zunächst einen Request mit den wesentlichen Informationen. Dieser Request wird vom issuer geprüft und ggf. signiert.
Die Regeln, die ein Zertifikat erfüllen muß, wird policy genannt.

3.5.4Einen Certificate-Request erzeugen

Der Besitzer eines public keys ( der aus einem private key erstellt werden kann ), erstellt einen Certificate Signing Request ( CSR ). Dabei wird der private key verwendet, ein public key erzeugt und mit dem Distinguished Name ( DN ) gemäß X.500 versehen.
Der DN enthält folgende Informationen :

Mit Hilfe des DN können bestimmte Regeln definiert werden ( policy ), wie solch ein Request von der CA verarbeitet wird. Ist der Antragsteller eine Privatfirma, so muß i.A. nichts von seinem DN mit dem DN der CA übereinstimmen. Ist der Antragsteller aber eine "Unter-CA" ( bei hierarchischen Strukturen ), so kann von der CA, die das Zertifikat ausstellt, verlangt werden, daß Teile des DNs mit Teilen ihres DNs übereinstimmen.
Vergleiche dazu die Abschnitte [ policy-match ] und [ policy-anything ] in der openssl.cnf.

Beispiel : Privatfirma (Bank of NSE) erstellt CSR
Voraussetzung : private key in einer Datei bonse_priv.pem
( openssl genrsa -out bonse_priv.pem 1024 )

thin1:/usr/share/ssl # openssl req -new -key bonse_priv.pem -out bonse.csr
Using configuration from /usr/share/ssl/openssl.cnf
You are about to be asked to enter 
information that will be incorporated into your certificate request.
What you are about to enter is what is called a Distinguished Name or a DN.
There are quite a few fields but you can leave some blank
For some fields there will be a default value,
If you enter '.', the field will be left
blank.
-----
Country Name (2 letter code) [AU]:DE
State or Province Name (full name) [Some-State]:Schleswig-Holstein
Locality Name (eg, city) []:Kiel
Organization Name (eg, company) [Internet
Widgits Pty Ltd]:Bank of NSE
Organizational Unit Name (eg, section) []:Security
Section
Common Name (eg, YOUR name) []:nseXX.nse
Email Address []:root@nseXX.nse

Bemerkung : Im Abschnitt [ req ] wurde die Variable attributes = req_attributes auskommentiert.
Die Datei mit dem Request hat folgenden Inhalt :

thin1:/usr/share/ssl # cat bonse.csr
-----BEGIN CERTIFICATE REQUEST-----
MIIB3jCCAUcCAQAwgZ0xCzAJBgNVBAYTAkRFMRswGQYDVQQIExJTY2hsZXN3aWct
SG9sc3RlaW4xDTALBgNVBAcTBEtpZWwxFDASBgNVBAoTC0Jhbmsgb2YgTlNFMRkw
FwYDVQQLExBTZWN1cml0eSBTZWN0aW9uMRIwEAYDVQQDEwluc2VYWC5uc2UxHTAb
BgkqhkiG9w0BCQEWDnJvb3RAbnNlWFgubnNlMIGfMA0GCSqGSIb3DQEBAQUAA4GN
ADCBiQKBgQDWCdNsAIYP9C6DNnNiX4UnP7sLtnNFTL82gh19uj61JGQaI70uKzRs
0NN1OKHH0tD4opejeuFjwrvZYkRH8q45hucyB47/3sQXVHTIbMO4051pizK8jzPc
MKspHD9ipxm80C/oXiAYjByMs4GdJvdLqLIeuVQNANIg2ZQqgji6swIDAQABoAAw
DQYJKoZIhvcNAQEEBQADgYEAF/AXGszKqGbq5ATohEWV91m2PQ/X4e6EPzWGPQRq
kFIonDbY2FdDw4rIovdFkf4uVE5zBs6mFHKv6bocLTYyYsOCi3fKqcBKVVgU1NNx
IqigypmomBKedm3ZKgnRY618XjvmaL2GX3zjvBL07qpBmsotLzGooTbeZKS5LChY
1OY=
-----END CERTIFICATE REQUEST-----

3.5.5Inhalte eines Certificate-Signing-Request

Die Datei mit dem Request hat folgenden Inhalt :

thin1:/usr/share/ssl # cat bonse.csr
-----BEGIN CERTIFICATE REQUEST-----
MIIB3jCCAUcCAQAwgZ0xCzAJBgNVBAYTAkRFMRswGQYDVQQIExJTY2hsZXN3aWct
SG9sc3RlaW4xDTALBgNVBAcTBEtpZWwxFDASBgNVBAoTC0Jhbmsgb2YgTlNFMRkw
FwYDVQQLExBTZWN1cml0eSBTZWN0aW9uMRIwEAYDVQQDEwluc2VYWC5uc2UxHTAb
BgkqhkiG9w0BCQEWDnJvb3RAbnNlWFgubnNlMIGfMA0GCSqGSIb3DQEBAQUAA4GN
ADCBiQKBgQDWCdNsAIYP9C6DNnNiX4UnP7sLtnNFTL82gh19uj61JGQaI70uKzRs
0NN1OKHH0tD4opejeuFjwrvZYkRH8q45hucyB47/3sQXVHTIbMO4051pizK8jzPc
MKspHD9ipxm80C/oXiAYjByMs4GdJvdLqLIeuVQNANIg2ZQqgji6swIDAQABoAAw
DQYJKoZIhvcNAQEEBQADgYEAF/AXGszKqGbq5ATohEWV91m2PQ/X4e6EPzWGPQRq
kFIonDbY2FdDw4rIovdFkf4uVE5zBs6mFHKv6bocLTYyYsOCi3fKqcBKVVgU1NNx
IqigypmomBKedm3ZKgnRY618XjvmaL2GX3zjvBL07qpBmsotLzGooTbeZKS5LChY
1OY=
-----END CERTIFICATE REQUEST-----

Dieser Inhalt kann lesbar gemacht werden

thin1:/usr/share/ssl # openssl req -in bonse.csr -text -noout
Using configuration from /usr/share/ssl/openssl.cnf
Certificate Request:
    Data:
        Version: 0 (0x0)
        Subject: C=DE, ST=Schleswig-Holstein, L=Kiel, O=Bank of NSE, 
                 OU=Security Section, CN=nseXX.nse/Email=root@nseXX.nse
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
            RSA Public Key: (1024 bit)
                Modulus (1024 bit):
                    00:d6:09:d3:6c:00:86:0f:f4:2e:83:36:73:62:5f:
                    85:27:3f:bb:0b:b6:73:45:4c:bf:36:82:1d:7d:ba:
                    3e:b5:24:64:1a:23:bd:2e:2b:34:6c:d0:d3:75:38:
                    a1:c7:d2:d0:f8:a2:97:a3:7a:e1:63:c2:bb:d9:62:
                    44:47:f2:ae:39:86:e7:32:07:8e:ff:de:c4:17:54:
                    74:c8:6c:c3:b8:d3:9d:69:8b:32:bc:8f:33:dc:30:
                    ab:29:1c:3f:62:a7:19:bc:d0:2f:e8:5e:20:18:8c:
                    1c:8c:b3:81:9d:26:f7:4b:a8:b2:1e:b9:54:0d:00:
                    d2:20:d9:94:2a:82:38:ba:b3
                Exponent: 65537 (0x10001)
        Attributes:
            a0:00
    Signature Algorithm: md5WithRSAEncryption
        17:f0:17:1a:cc:ca:a8:66:ea:e4:04:e8:84:45:95:f7:59:b6:
        3d:0f:d7:e1:ee:84:3f:35:86:3d:04:6a:90:52:28:9c:36:d8:
        d8:57:43:c3:8a:c8:a2:f7:45:91:fe:2e:54:4e:73:06:ce:a6:
        14:72:af:e9:ba:1c:2d:36:32:62:c3:82:8b:77:ca:a9:c0:4a:
        55:58:14:d4:d3:71:22:a8:a0:ca:99:a8:98:12:9e:76:6d:d9:
        2a:09:d1:63:ad:7c:5e:3b:e6:68:bd:86:5f:7c:e3:bc:12:f4:
        ee:aa:41:9a:ca:2d:2f:31:a8:a1:36:de:64:a4:b9:2c:28:58:
        d4:e6
thin1:/usr/share/ssl #

Version : ?
Subject : Distinguished Name gemäß x.500
Algorithmus : RSA
Keysize : 1024 Bit
Modulus und Exponent : Bestandteile des public-keys bei RSA
Attribute : ?
Signaturalgorithmus : md5 mit RSA-Verschlüsselung
Hashwert nach MD5

3.5.6RootCA

Root CA - Selfsigned Certificate

openssl req -new -x509 -key CA_PRIV.pem -out CA_CERT.pem

Beschreibung
Die RootCA braucht zunächst ein Zertifikat, mit dem es arbeiten kann. Nur sie selbst kann dieses signieren, und zwar nur mit ihrem private key.
Notwendig ist das Erstellen einer Datei "serial" mit Inhalt "00" als Seriennummer des nächsten Zertifikats.¹

Ausgabeformate

Standardmäßig ist das Ausgabeformat PEM ( Dateiendung .pem ).
Es kann das Ausgabeformat DER gewählt werden ( -outform DER ).
Die Formate können ineinander konvertiert werden :

openssl x509 -inform DER -in 00.der  -outform PEM -out 00.pem

Das Ausgabeformat ist entscheidend bei der Verwendung des Zertifikates durch eine Anwendung. Z. B. verwendet FreeSWAN ( eine IPSEC-Implementation ) das DER-Format.
MS Outlook 2000 (9.0.0.x) kann DER importieren.
MSIE 5 kann PKCS12 erkennen (als PFX) und importieren.
,
Zertifikate im PEM-Format können in das PKCS12-Format( .p12 ) exportiert werden :

openssl pkcs12 -export -in 00.pem -inkey 00_key.pem -out 00.p12

Dabei kann ein Export-Passwort mitgegeben werden.

Verlinkung mit dem Hashwert

Für die Verwaltung von Zertifikaten wird mit einem symbolic link auf das Zertifikat gearbeitet. Der Name des links ergibt sich aus dem Hashwert der Zertifikatsdatei gefolgt von ".0".
Der Hashwert einer Datei ergibt sich aus

openssl x509 -hash -in 00.pem -noout

Damit kann der link unter Verwendung von Backticks erzeugt werden :

ln -s 00.pem `openssl x509 -hash -in 00.pem -noout`.0

¹ : Das RootCA-Zertifikat bekommt die Serial 00 ( hexadezimal durchnummeriert ), muß in ein Verzeichnis gemäß openssl.cnf kopiert und mit seinem Hashwert als Dateinamen verlinkt werden. Diese Aktionen sind zur späteren Verwendung notwendig und werden hier zunächst nicht behandelt.

3.6OpenSSL Direkt 1

Kurzer Überblick über die Möglichkeiten von OpenSSL ( Verschlüsselung )

Symmetrische Verschlüsselung

openssl enc -e -des -in passwd -out encrypted_passwd

Möglichkeiten:

• Verfahren : DES 2DES 3DES Blowfish IDEA CAST5 RC2
• Modi : CBC CFB OFB
• Password - geschützte Datei ( Password = Schlüssel )

Schlüsselerzeugung RSA ( genrsa )

openssl genrsa -des -out privkey.pem 1024

Möglichkeiten:

• RSA - privatekey mit wählbarer Schlüssellänge ( hier : 1024 )
• optionale Verschlüsselung mit DES 3DES IDEA (Passphrase > 4 Zeichen)

Message Digest ( dgst )

openssl dgst -c -out passwd.fipri -md5 passwd

Möglichkeiten:

• Hashalgorithmen: MD5 MD2 SHA-1 SHA RIPEMD160 MDC2
• Byteweise Ausgabe mit -c ( Doppelpunkt-Trennung )
• optionales Speichern in Datei

Public Key Erzeugung ( rsa )

openssl rsa -pubout -in priv_key.pem -out pub_key.pem

Möglichleiten:

• Erzeugt public key aus private key ( -pubout )
• Verschlüsselt public key mit DES 3DES IDEA ( optional )

Signaturen ( dgst )

openssl dgst -sign privkey.pem -out sig_passwd passwd

Möglichkeiten:

• Signiert Dateien ( letzter Parameter ) mit private key ( -sign privkey.pem )
• Erstellt Datei mit verschlüsselter Signatur ( ohne DATA ! )
• Verändert nicht die Daten ( Signatur kann seperat geschickt werden )
• Signatur kann mit dem public key verifiziert werden

  openssl dgst -verify pubkey.pem -signature sig_passwd passwd

• Signatur kann mit dem privat key verifiziert werden

  openssl dgst -prverify privkey.pem -signature sig_passwd passwd

3.7OpenSSL Direkt 2

Kurzer Überblick über die Möglichkeiten von OpenSSL im Bereich der Zertifikate

Arbeitsverzeichnis ist /usr/share/ssl
Konfigurationsdatei openssl.cnf :
[ CA_default ]
dir = .

Root CA - Selfsigned Certificate Request

openssl req -new -x509 -key CA_PRIV.pem -out CA_CERT.crt

Beschreibung
Die RootCA braucht zunächst ein Zertifikat, mit dem es arbeiten kann. Nur sie selbst kann dieses signieren, und zwar nur mit ihrem private key.
Notwendig ist das Erstellen einer Datei "serial" mit Inhalt "01" als Seriennummer des nächsten Zertifikats.¹

Certificate Requests ( Server / user / Sub-CA )

Voraussetzung : keine, hier : Antragsteller besitzt private key

openssl req -new -key BOK_PRIV.pem -out BOK_CSR.csr

Das Kommando erstellt aus dem private key den public key und daraus einen CSR. Die X509-konformen Einträge (countryName ...) sind mit der CA abzusprechen ( vgl. policy, die die CA verwendet, gilt insbesondere bei Sub-CAs ).
Die Datei BOK_CSR.csr wird der CA zur Zertifizierung übergeben.

Zertifizierungen

openssl ca  -keyfile CA_PRIV.pem -in BOK_CSR.csr

Beschreibung
Ohne weitere Angaben wird zum Signieren das RootCA - Zertifikat im Pfad laut openssl.cnf genommen.
Mit -cert CA_CERT.crt kann der Pfad explizit angegeben werden.

Gleiches gilt für -key geheim ( Passphrase CA_PRIV.pem )

openssl ca -keyfile CA_PRIV.pem -key geheim -cert CA_CERT.crt -in BOK_CSR.csr

Neue Zertifikate werden automatisch in einem Verzeichnis gemäß openssl.cnf ("newcerts", muß angelegt werden) gespeichert.

---

¹ : Das RootCA-Zertifikat bekommt die Serial 00 ( hexadezimal durchnummeriert ), muß in ein Verzeichnis gemäß openssl.cnf kopiert und mit seinem Hashwert als Dateinamen verlinkt werden. Diese Aktionen sind zur späteren Verwendung notwendig und werden hier zunächst nicht behandelt.

4Literatur

4.1Bücher

4.2Tutorials

4.3Gesetze